Publications
Characterizing out-of-distribution generalization of neural networks: application to the disordered Su-Schrieffer-Heeger model
K. Cybiński, M. Płodzień, M. Tomza, M. Lewenstein, A. Dauphin, & A. Dawid
Mach. Learn.: Sci. Technol. 6, 015014 (2025)
Summary
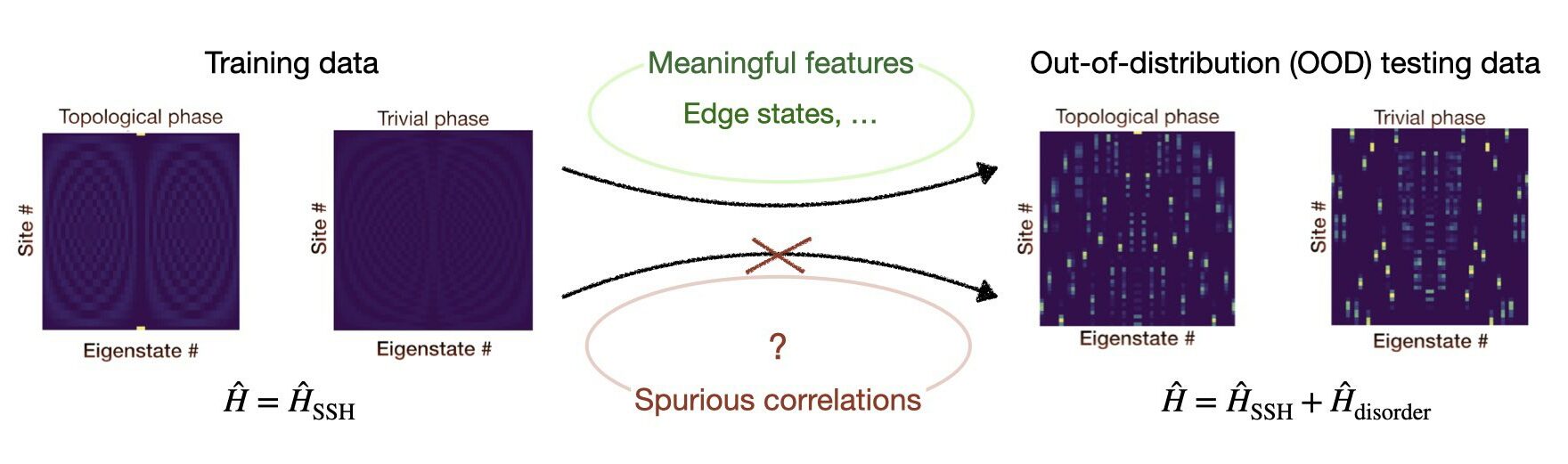
Machine learning (ML) is a promising tool for the detection of phases of matter. However, ML models are also known for their black-box construction, which hinders understanding of what they learn from the data and makes their application to novel data risky. Moreover, the central challenge of ML is to ensure its good generalization abilities, i.e., good performance on data outside the training set. Here, we show how the informed use of an interpretability method called class activation mapping (CAM), and the analysis of the latent representation of the data with the principal component analysis (PCA) can increase trust in predictions of a neural network (NN) trained to classify quantum phases. In particular, we show that we can ensure better out-of-distribution generalization in the complex classification problem by choosing such an NN that, in the simplified version of the problem, learns a known characteristic of the phase. We show this on an example of the topological Su-Schrieffer-Heeger (SSH) model with and without disorder, which turned out to be surprisingly challenging for NNs trained in a supervised way. This work is an example of how the systematic use of interpretability methods can improve the performance of NNs in scientific problems.
Learning interactions between Rydberg atoms
O. Simard*, A. Dawid*, J. Tindall, M. Ferrero, A. M. Sengupta, A. Georges
arXiv:2412.12019
Summary
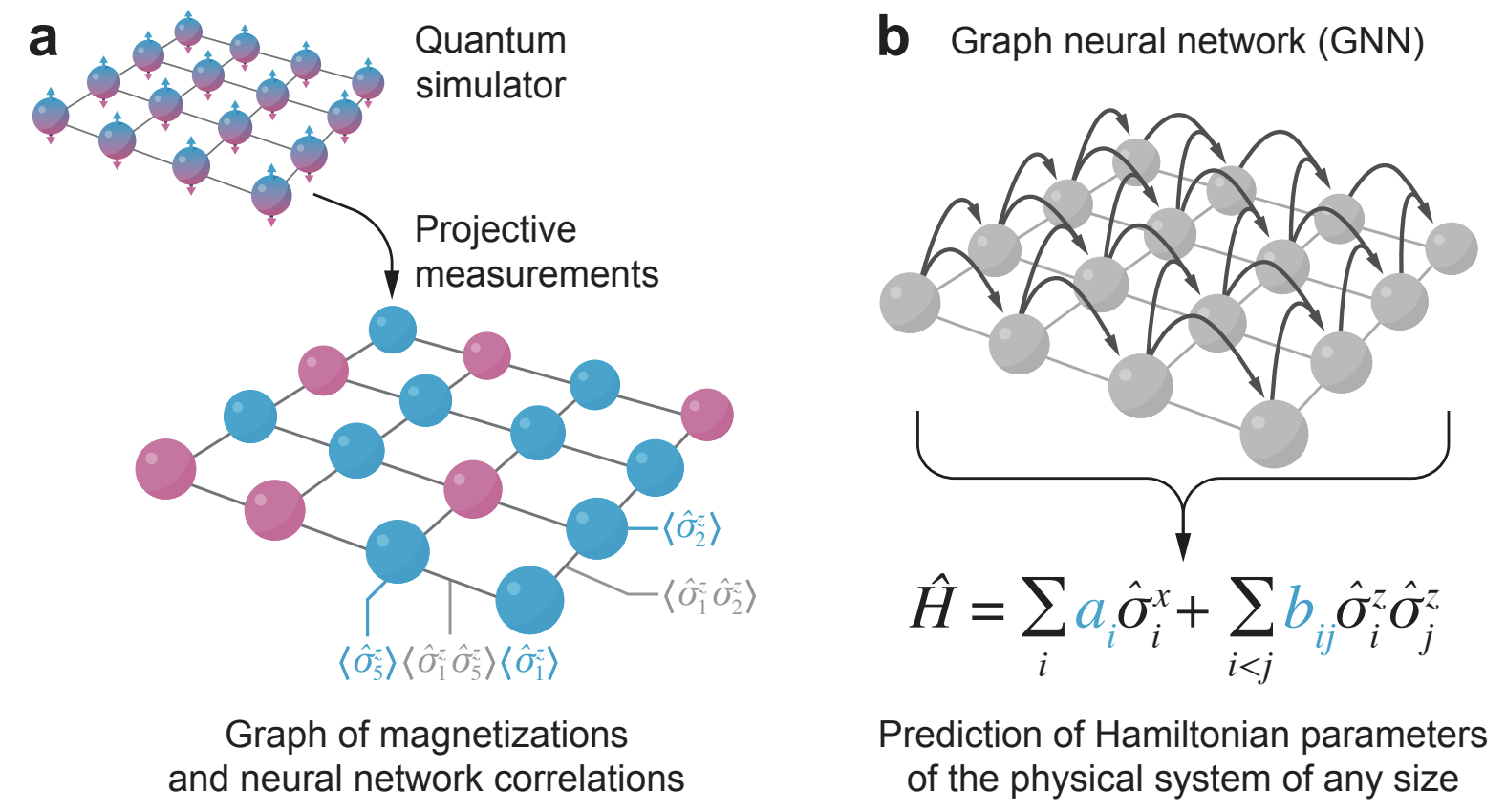
Quantum simulators have the potential to solve quantum many-body problems that are beyond the reach of classical computers, especially when they feature long-range entanglement. To fulfill their prospects, quantum simulators must be fully controllable, allowing for precise tuning of the microscopic physical parameters that define their implementation. We consider Rydberg-atom arrays, a promising platform for quantum simulations. Experimental control of such arrays is limited by the imprecision on the optical tweezers positions when assembling the array, hence introducing uncertainties in the simulated Hamiltonian. In this work, we introduce a scalable approach to Hamiltonian learning using graph neural networks (GNNs). We employ the Density Matrix Renormalization Group (DMRG) to generate ground-state snapshots of the transverse field Ising model realized by the array, for many realizations of the Hamiltonian parameters. Correlation functions reconstructed from these snapshots serve as input data to carry out the training. We demonstrate that our GNN model has a remarkable capacity to extrapolate beyond its training domain, both regarding the size and the shape of the system, yielding an accurate determination of the Hamiltonian parameters with a minimal set of measurements. We prove a theorem establishing a bijective correspondence between the correlation functions and the interaction parameters in the Hamiltonian, which provides a theoretical foundation to our learning algorithm. Our work could open the road to feedback control of the positions of the optical tweezers, hence providing a decisive improvement of analog quantum simulators.
2024
Popular science
Ktokolwiek widział, ktokolwiek wie! Ukradziono Nagrodę Nobla z fizyki! [ENG: Beware! The Nobel Prize in physics got stolen!]
A. Dawid
Postępy Fizyki, 75(3-4), 12-16 (2024)
Summary
Nagroda Nobla z fizyki w 2024 została przyznana Johnowi J. Hopfieldowi z Uniwersytetu w Princeton i Geoffrey’owi E. Hintonowi z Uniwersytetu w Toronto za fundamentalne odkrycia i wynalazki umożliwiające uczenie maszynowe przy użyciu sztucznych sieci neuronowych. Choć wywołała kontrowersje wśród naukowców, to wpisuje się ona w trend nagradzania twórców nowych przyrządów do badania świata, a takim staje się ostatnio uczenie maszynowe. Opisuję w tym artykule dokonania noblistów, w szczególności sieć Hopfielda i maszynę Boltzmanna i wyjaśniam, jak różnią się od współczesnego paradygmatu uczenia maszynowego. Zwracam też uwagę na ograniczenia sieci neuronowych, a także ekscytujący dwukierunkowy wpływ, jaki wciąż mają na siebie nawzajem uczenie maszynowe i fizyka.
Speak so a physicist can understand you! TetrisCNN for detecting phase transitions and order parameters
K. Cybiński, J. Enouen, A. Georges, & A. Dawid
NeurIPS 2024 Workshop “Machine Learning and the Physical Sciences”, arXiv:2411.02237
Summary
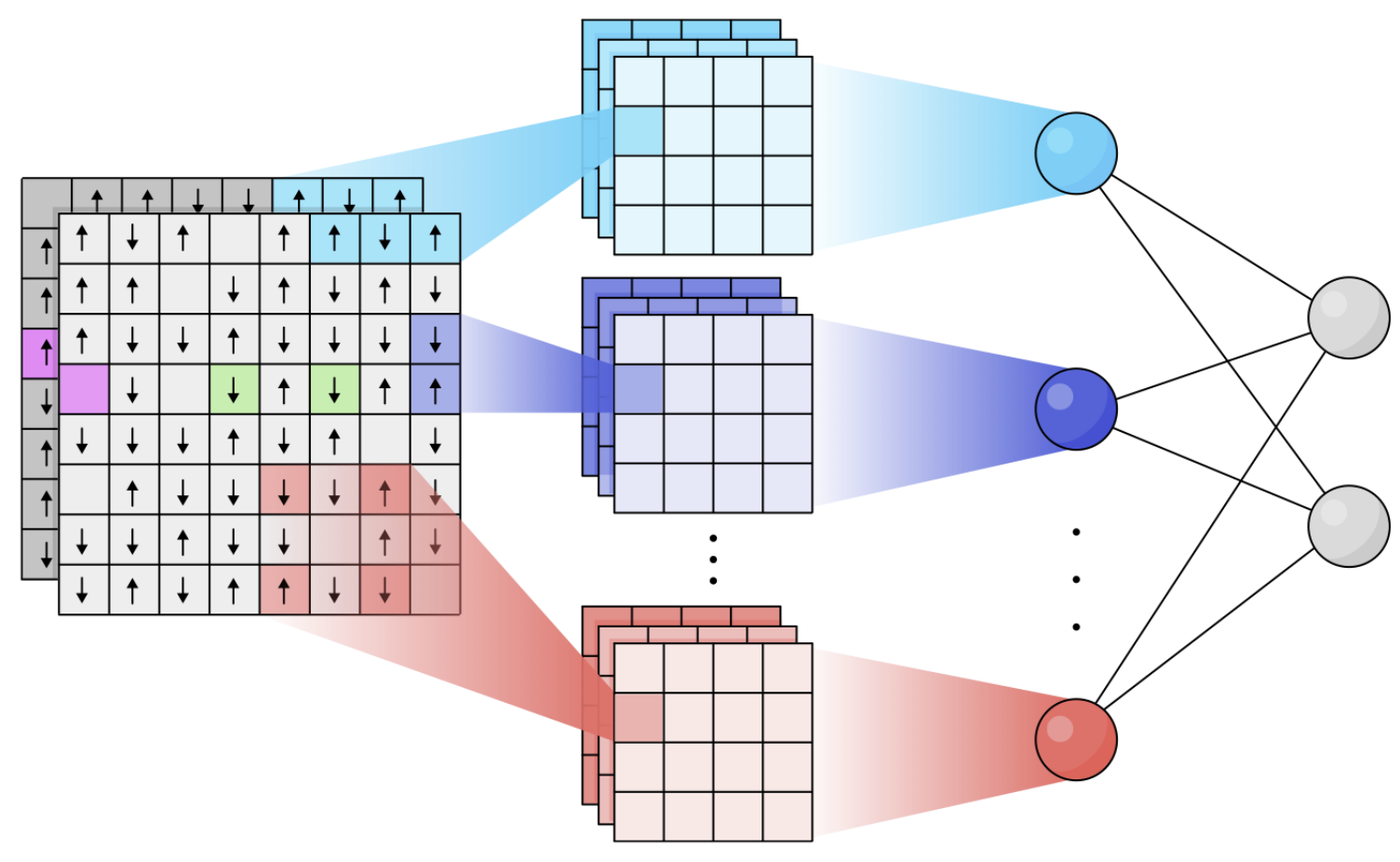
Recently, neural networks (NNs) have become a powerful tool for detecting quantum phases of matter. Unfortunately, NNs are black boxes and only identify phases without elucidating their properties. Novel physics benefits most from insights about phases, traditionally extracted in spin systems using spin correlators. Here, we combine two approaches and design TetrisCNN, a convolutional NN with parallel branches using different kernels that detects the phases of spin systems and expresses their essential descriptors, called order parameters, in a symbolic form based on spin correlators. We demonstrate this on the example of snapshots of the one-dimensional transverse-field Ising model taken in various bases. We show also that TetrisCNN can detect more complex order parameters using the example of two-dimensional Ising gauge theory. This work can lead to the integration of NNs with quantum simulators to study new exotic phases of matter.
Deconstructing the Goldilocks Zone of Neural Network Initialization
A. Vysogorets, A. Dawid, & J. Kempe
ICML 2024, arXiv:2402.03579
Summary
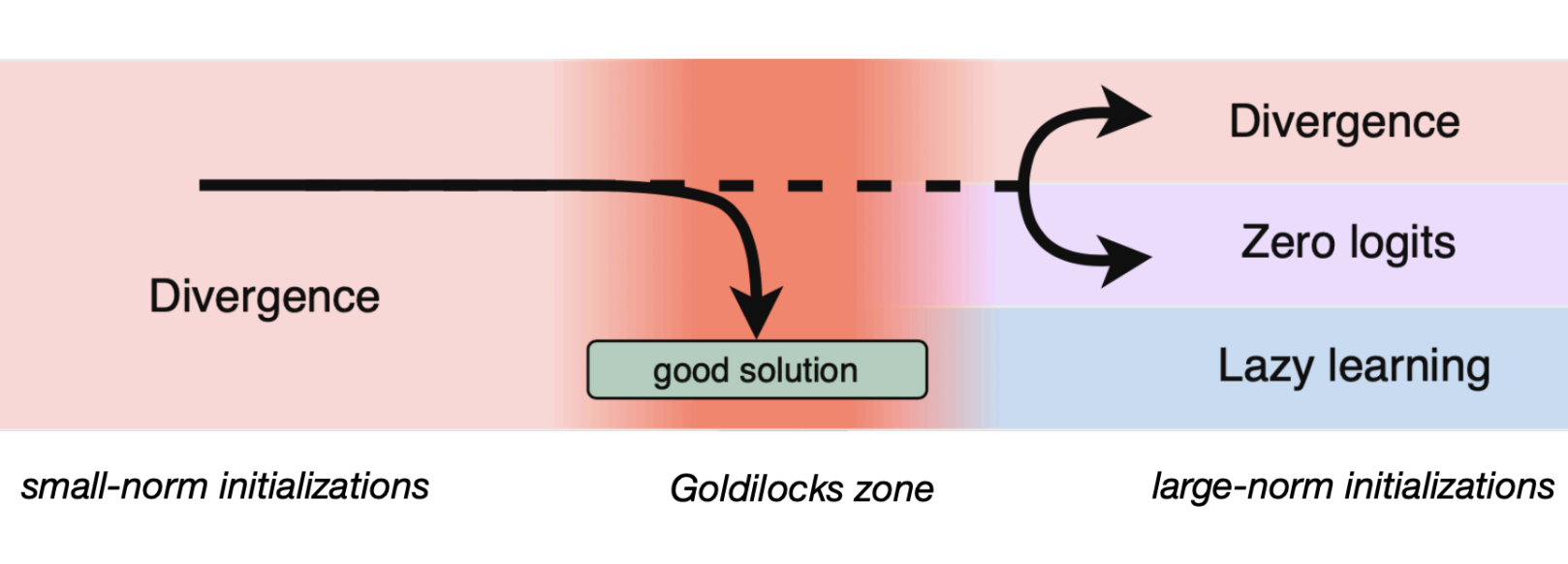
The second-order properties of the training loss have a massive impact on the optimization dynamics of deep learning models. Fort & Scherlis (2019) discovered that a high positive curvature and local convexity of the loss Hessian are associated with highly trainable initial points located in a region coined the “Goldilocks zone”. Only a handful of subsequent studies touched upon this relationship, so it remains largely unexplained. In this paper, we present a rigorous and comprehensive analysis of the Goldilocks zone for homogeneous neural networks. In particular, we derive the fundamental condition resulting in non-zero positive curvature of the loss Hessian and argue that it is only incidentally related to the initialization norm, contrary to prior beliefs. Further, we relate high positive curvature to model confidence, low initial loss, and a previously unknown type of vanishing cross-entropy loss gradient. To understand the importance of positive curvature for trainability of deep networks, we optimize both fully-connected and convolutional architectures outside the Goldilocks zone and analyze the emergent behaviors. We find that strong model performance is not necessarily aligned with the Goldilocks zone, which questions the practical significance of this concept.
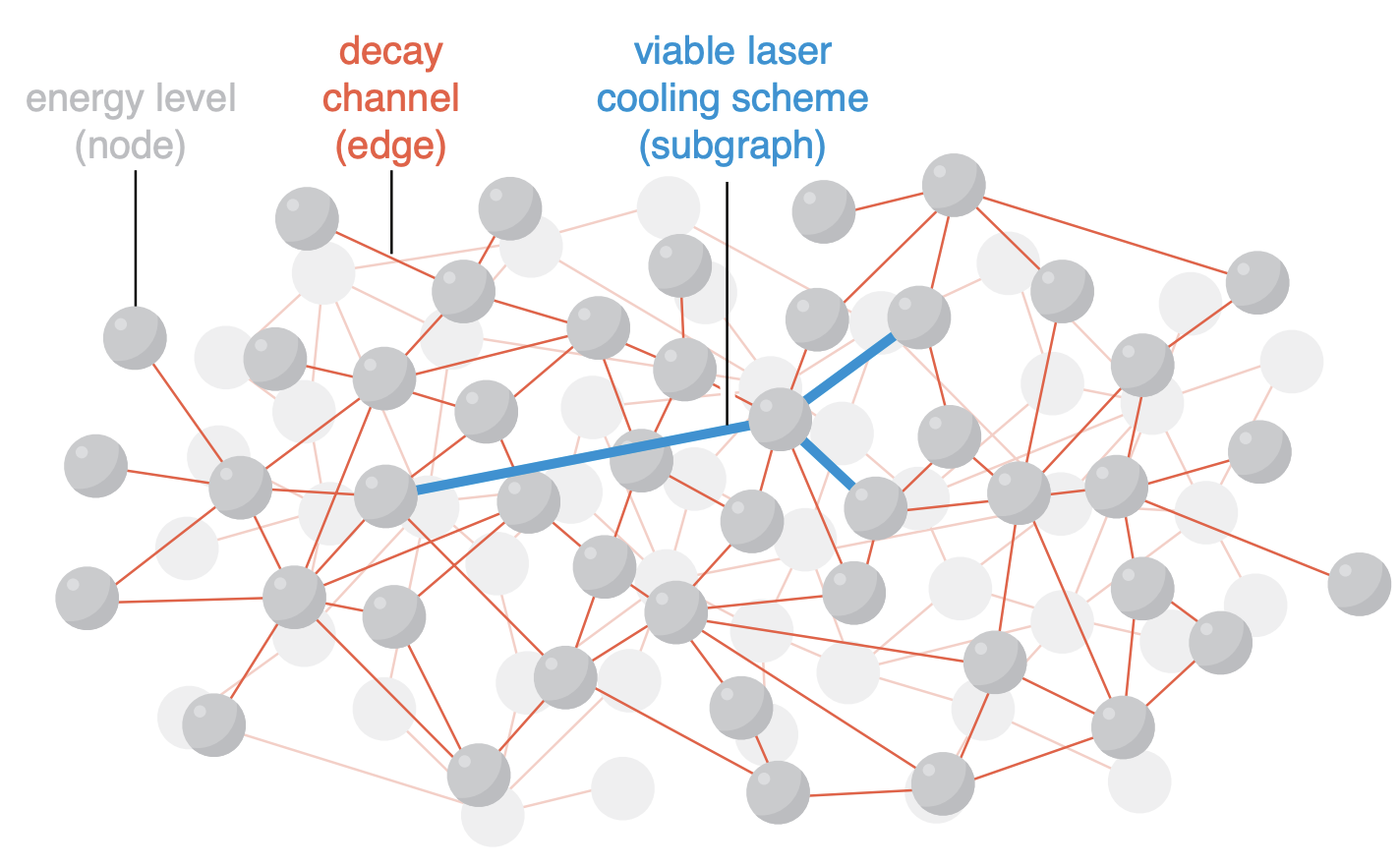
Automated detection of laser cooling schemes for ultracold molecules
A. Dawid, N. Bigagli, D. W. Savin, & S. Will
arXiv:2311.08381 (2023)
Summary
One of the demanding frontiers in ultracold science is identifying laser cooling schemes for complex atoms and molecules, out of their vast spectra of internal states. Motivated by a need to expand the set of available ultracold molecules for applications in fundamental physics, chemistry, astrochemistry, and quantum simulation, we propose and demonstrate an automated graph-based search approach for viable laser cooling schemes. The method is time efficient and the outcomes greatly surpass the results of manual searches used so far. We discover new laser cooling schemes for C2, OH+, CN, YO, and CO2 that can be viewed as surprising or counterintuitive compared to previously identified laser cooling schemes. In addition, a central insight of this work is that the reinterpretation of quantum states and transitions between them as a graph can dramatically enhance our ability to identify new quantum control schemes for complex quantum systems. As such, this approach will also be applicable to complex atoms and, in fact, any complex many-body quantum system with a discrete spectrum of internal states.
2023
NeurIPS workshop
Unveiling the Hessian’s Connection to the Decision Boundary
M. Sabanayagam, F. Behrens, U. Adomaityte, & A. Dawid
NeurIPS 2023 Workshop on Mathematics of Modern Machine Learning, arXiv:2306.07104
Summary
Understanding the properties of well-generalizing minima is at the heart of deep learning research. On the one hand, the generalization of neural networks has been connected to the decision boundary complexity, which is hard to study in the high-dimensional input space. Conversely, the flatness of a minimum has become a controversial proxy for generalization. In this work, we provide the missing link between the two approaches and show that the Hessian top eigenvectors characterize the decision boundary learned by the neural network. Notably, the number of outliers in the Hessian spectrum is proportional to the complexity of the decision boundary. Based on this finding, we provide a new and straightforward approach to studying the complexity of a high-dimensional decision boundary; show that this connection naturally inspires a new generalization measure; and finally, we develop a novel margin estimation technique which, in combination with the generalization measure, precisely identifies minima with simple wide-margin boundaries. Overall, this analysis establishes the connection between the Hessian and the decision boundary and provides a new method to identify minima with simple wide-margin decision boundaries.
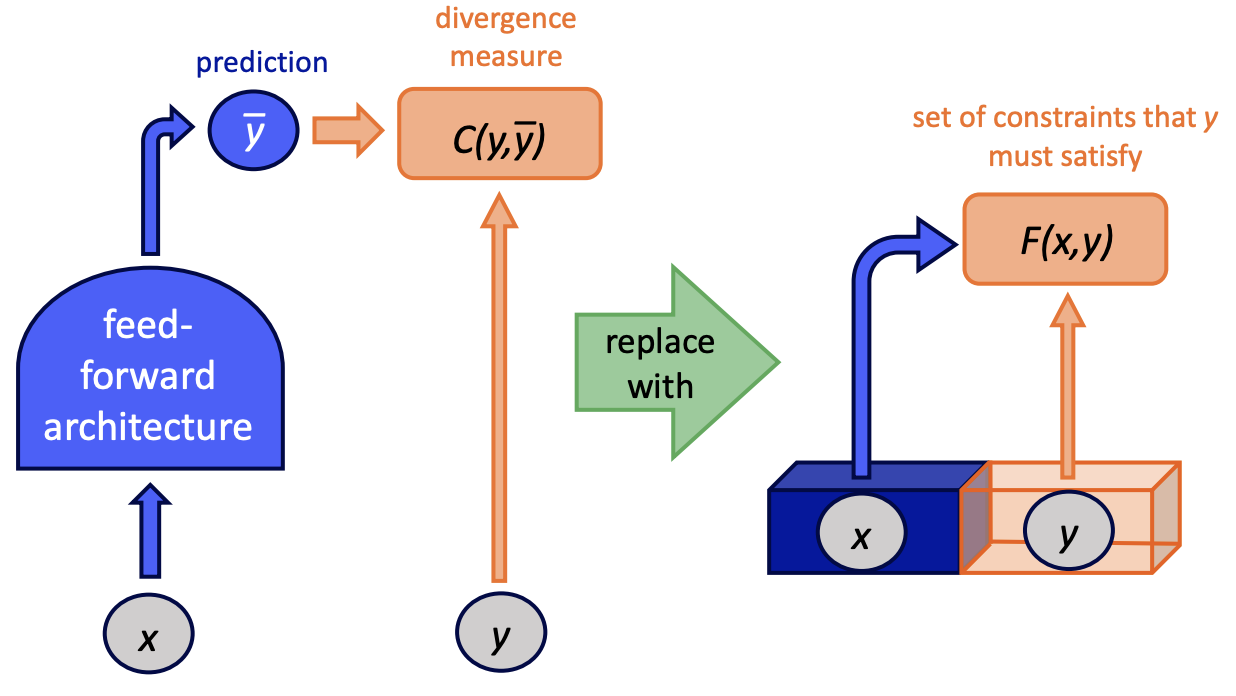
Introduction to Latent Variable Energy-Based Models: A Path Towards Autonomous Machine Intelligence
A. Dawid & Yann LeCun
J. Stat. Mech. 2024, 104011 (2024)
Summary
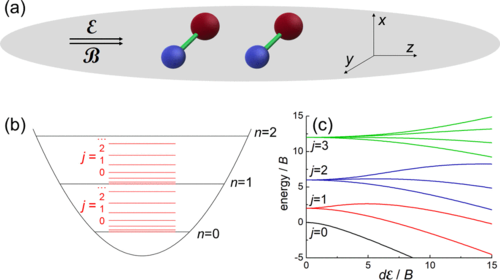
Two highly magnetic atoms in a one-dimensional harmonic trap
M. Suchorowski, A. Dawid & M. Tomza
Phys. Rev. A 106, 043324 (2022)
Summary
We investigate the properties of two interacting ultracold polar molecules described as distinguishable quantum rigid rotors, trapped in a one-dimensional harmonic potential. The molecules interact via a multichannel two-body contact potential, incorporating the short-range anisotropy of intermolecular interactions including dipole-dipole interaction. The impact of external electric and magnetic fields resulting in Stark and Zeeman shifts of molecular rovibrational states is also investigated. Energy spectra and eigenstates are calculated by means of the exact diagonalization. The importance and interplay of the molecular rotational structure, anisotropic interactions, spin-rotation coupling, electric and magnetic fields, and harmonic trapping potential are examined in detail, and compared to the system of two harmonically trapped distinguishable atoms. The presented model and results may provide microscopic parameters for molecular many-body Hamiltonians, and may be useful for the development of bottom-up molecule-by-molecule assembled molecular quantum simulators.
Modern applications of machine learning in quantum sciences
A. Dawid, J. Arnold*, B. Requena*, A. Gresch*, M. Płodzień, K. Donatella, K. A. Nicoli, P. Stornati, R. Koch, M. Büttner, R. Okuła, G. Muñoz-Gil, R. A. Vargas-Hernández, A. Cervera-Lierta, J. Carrasquilla, V. Dunjko, M. Gabrié, P. Huembeli, E. van Nieuwenburg, F. Vicentini, L. Wang, S. J. Wetzel, G. Carleo, E. Greplová, R. Krems, F. Marquardt, M. Tomza, M. Lewenstein & A. Dauphin
arXiv:2204.04198 (2022)
Summary
What happens if you combine the best experts in the field with hard-working and ambitious students? You get a Book. We provide a comprehensive introduction to the most recent advances in the application of machine learning methods in quantum sciences. We cover here the use of deep learning and kernel methods in supervised, unsupervised, and reinforcement learning algorithms for phase classification, representation of many-body quantum states, quantum feedback control, and quantum circuits optimization. Moreover, we introduce and discuss more specialized topics such as differentiable programming, generative models, statistical approach to machine learning, and quantum machine learning.
Controlling the dynamics of ultracold polar molecules in optical tweezers
M. Sroczyńska, A. Dawid, M. Tomza, T. Calarco, Z. Idziaszek & K. Jachymski
New J. Phys. 24, 015001 (2022)
Summary
Ultracold molecules trapped in optical tweezers show great promise for the implementation of quantum technologies and precision measurements. We study a prototypical scenario where two interacting polar molecules placed in separate traps are controlled using an external electric field. This, for instance, enables a quantum computing scheme in which the rotational structure is used to encode the qubit states. We estimate the typical operation timescales needed for state engineering to be in the range of few microseconds. We further underline the important role of the spatial structure of the two-body states, with the potential for significant gate speedup employing trap-induced resonances.
Hessian-based toolbox for reliable and interpretable machine learning in physics
A. Dawid, P. Huembeli, M. Tomza, M. Lewenstein & A. Dauphin
Mach. Learn.: Sci. Technol. 3, 015002 (2022)
Summary
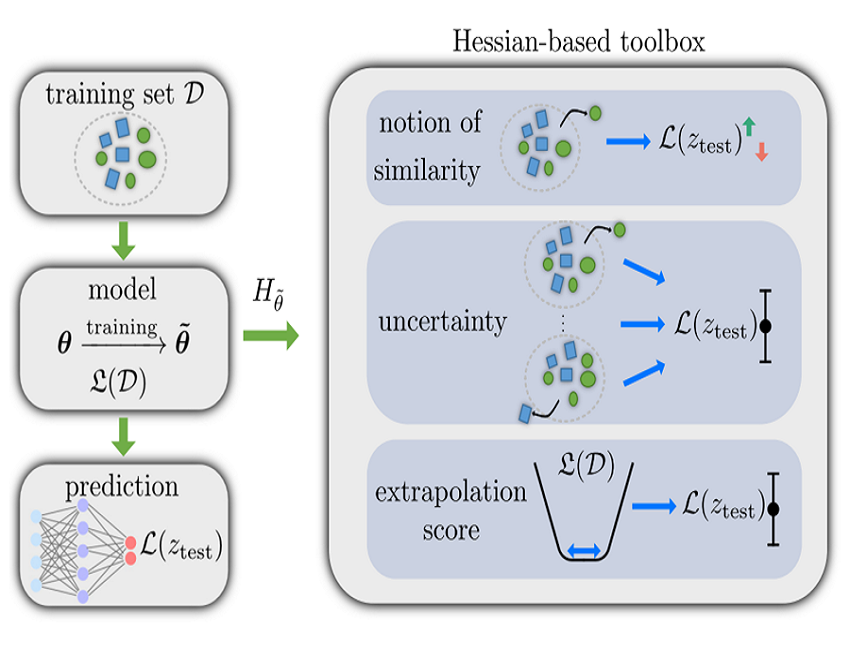
Mach. Learn.: Sci. Technol. 3 015002 – Do you lack confidence in your machine learning model? We can help with that! Ask the Hessian of the training loss, and you will know: (1) which data your neural network (NN) views as similar, (2) if a NN extrapolates a lot, (3) error bars of your test loss.
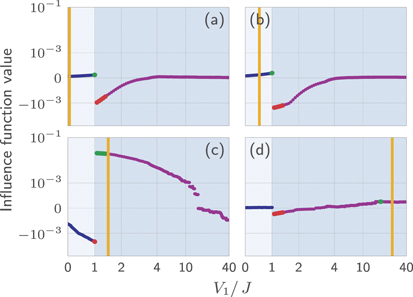
Unsupervised machine learning of topological phase transitions from experimental data
N. Käming*, A. Dawid*, K. Kottmann*, M. Lewenstein, K. Sengstock, A. Dauphin & C. Weitenberg
Mach. Learn.: Sci. Technol. 2, 035037 (2021)
Summary
Mach. Learn.: Sci. Technol. 2 035037 – Automated detection of quantum phases is especially challenging when dealing with experimental data and topological models. Here, we tackle both challenges at the same time! We show that many unsupervised techniques are insufficient to detect topological phases from experimental data and deliver the final blow with influence functions!
Magnetic properties and quench dynamics of two interacting ultracold molecules
A. Dawid & M. Tomza
Phys. Chem. Chem. Phys. 22, 28140–28153 (2020)
Summary
We theoretically investigate the magnetic properties and nonequilibrium dynamics of two interacting ultracold polar and paramagnetic molecules in a one-dimensional harmonic trap in external electric and magnetic fields. The molecules interact via a multichannel two-body contact potential, incorporating the short-range anisotropy of intermolecular interactions. We show that various magnetization states arise from the interplay of the molecular interactions, electronic spins, dipole moments, rotational structures, external fields, and spin–rotation coupling. The rich magnetization diagrams depend primarily on the anisotropy of the intermolecular interaction and the spin–rotation coupling. These specific molecular properties are challenging to calculate or measure. Therefore, we propose the quench dynamics experiments for extracting them from observing the time evolution of the analyzed system. Our results indicate the possibility of controlling the molecular few-body magnetization with the external electric field and pave the way towards studying the magnetization of ultracold molecules trapped in optical tweezers or optical lattices and their application in quantum simulation of molecular multichannel many-body Hamiltonians and quantum information storing.
Phase detection with neural networks: interpreting the black box
A. Dawid, P. Huembeli, M. Tomza, M. Lewenstein & A. Dauphin
New J. Phys. 22, 115001 (2020)
Summary
Neural networks (NNs) usually hinder any insight into the reasoning behind their predictions. We demonstrate how influence functions can unravel the black box of NN when trained to predict the phases of the one-dimensional extended spinless Fermi–Hubbard model at half-filling. Results provide strong evidence that the NN correctly learns an order parameter describing the quantum transition in this model. We demonstrate that influence functions allow to check that the network, trained to recognize known quantum phases, can predict new unknown ones within the data set. Moreover, we show they can guide physicists in understanding patterns responsible for the phase transition. This method requires no a priori knowledge on the order parameter, has no dependence on the NN’s architecture or the underlying physical model, and is therefore applicable to a broad class of physical models or experimental data.
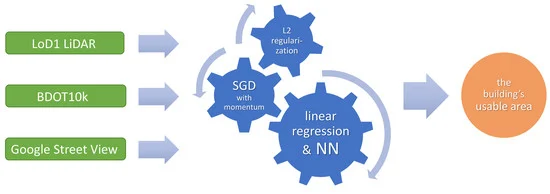
Estimation of usable area of flat-roof residential buildings using topographic data with machine learning methods
L. Dawid, M. Tomza & A. Dawid
Remote Sens. 11, 2382 (2019)
Summary
The real estate appraisal largely consists of estimating the property’s value based on the transaction prices of similar buildings with the usable area being one of the main comparative units. A Polish appraiser finds data mentioned in the Price and Value Register (PVR). However, one of the authors’ previous studies indicated that the PVR contained highly incomplete information on usable area of residential buildings rendering it impractical for real estate appraisal purposes. Here, we propose a machine learning method to estimate the usable area of flat-roof residential buildings based on Light Detection and Ranging (LiDAR) data as well as the Database of Topographic Objects (BDOT10k). First, we train models with different architectures on the exact project data of residential buildings available online, obtained mostly from the design offices Lipińscy and Archon. Then, we apply trained algorithms on available residential building in Koszalin, Poland, using BDOT10k and LoD1 standard LiDAR data, and compare the results with usable area reported in PVR. Results show that the usable area of flat-roof houses without garages and extensions can be calculated with great accuracy up to 4%, while for more complex flat-roof buildings-up to 4–10%, depending on how detailed data are available. The model may be used by real estate appraisers to approximate the unknown usable area of residential buildings with known transaction prices, and as such increase the number of properties that can be compared to the evaluated real estate. To estimate the usable area of buildings with more complex roofs, a higher standard of LiDAR data is needed.
Two ultracold interacting molecules in a one-dimensional harmonic trap
A. Dawid, M. Lewenstein & M. Tomza
Phys. Rev. A 97. (Editors’ Suggestion), 063618 (2018)
Summary
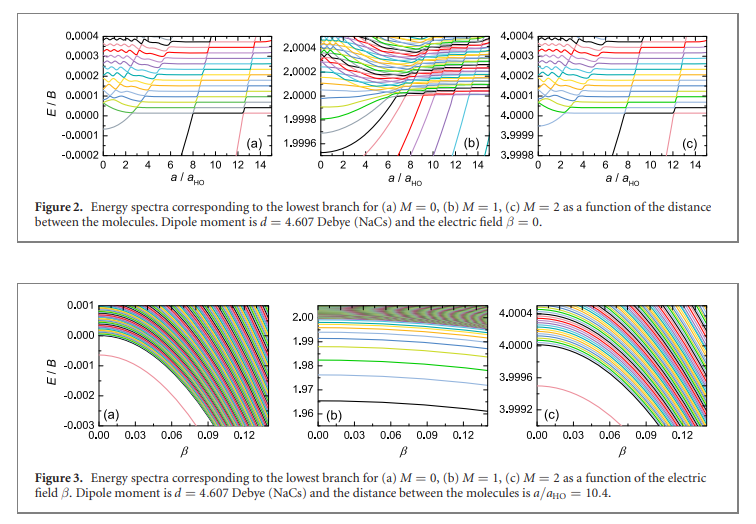
We investigate the properties of two interacting ultracold polar molecules described as distinguishable quantum rigid rotors, trapped in a one-dimensional harmonic potential. The molecules interact via a multichannel two-body contact potential, incorporating the short-range anisotropy of intermolecular interactions including dipole-dipole interaction. The impact of external electric and magnetic fields resulting in Stark and Zeeman shifts of molecular rovibrational states is also investigated. Energy spectra and eigenstates are calculated by means of the exact diagonalization. The importance and interplay of the molecular rotational structure, anisotropic interactions, spin-rotation coupling, electric and magnetic fields, and harmonic trapping potential are examined in detail, and compared to the system of two harmonically trapped distinguishable atoms. The presented model and results may provide microscopic parameters for molecular many-body Hamiltonians, and may be useful for the development of bottom-up molecule-by-molecule assembled molecular quantum simulators.
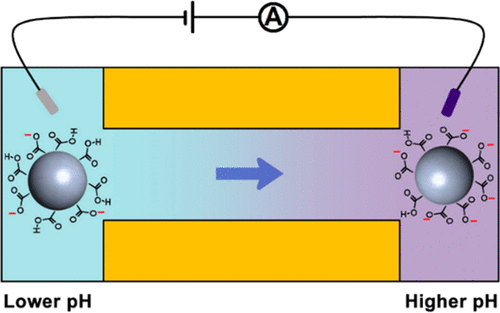
Experimental investigation of dynamic deprotonation / protonation of highly charged particles
Y. Qiu, A. Dawid & Z. Siwy
J. Phys. Chem. C 121, 6255–6263 (2017)
Summary
Single pores have found application in detecting and characterizing individual objects such as cells, particles, and even individual molecules. The experimental approach, called resistive-pulse technique, is often performed at symmetric electrolyte conditions so that the properties of the passing object remain constant in the course of measurement and translocation. Here we report experiments with highly charged mesoparticles passing through pores placed in contact with a pH gradient and demonstrate that this setup allows probing protonation and deprotonation of the particles. On the basis of fast diffusion of protons and submillisecond deprotonation/protonation kinetics of carboxyl groups, we expected that the particles would change their ionization state within a few milliseconds. However, our results show that the kinetics of protonation and deprotonation of the highly charged particles is significantly slower and exceeds 100 ms. We hypothesize that condensation of counterions that occurs on the particles at higher pH is responsible for the modified rates of protonation. The slowed-down deprotonation is attributed to modified local pH of the solution next to a highly charged surface. In addition, we show how electroosmotic flow of neutral particles through a pore in contact with pH gradient can probe modulations of local surface charge properties of the pore by voltage polarity.